Calculating the F-Fingerprint to compare crystal structures¶
The F-Fingerprint was introduced by Oganov and Valle in doi:10.1063/1.3079326 and doi:10.1107/S0108767310026395. The definition is based on the pair-wise partial radial distribution function.
First we create two crystals with ase:
[1]:
from ase.spacegroup import crystal
### GaAs
a = 4.066 * 2.0
GaAs_prim = crystal(
("Ga", "As"),
basis=((0.0, 0.0, 0.0), (0.75, 0.75, 0.75)),
spacegroup=216,
cellpar=[a, a, a, 90, 90, 90],
primitive_cell=True,
)
GaAs_conv = crystal(
("Ga", "As"),
basis=((0.0, 0.0, 0.0), (0.75, 0.75, 0.75)),
spacegroup=216,
cellpar=[a, a, a, 90, 90, 90],
primitive_cell=False,
)
We have created two times the same materials, but using different unit cells. GaAs_prim is the crystal structure with the primitive unit cell and GaAs_conv is uses conventional unit cell. We can print the crystal structures to visualize them with e.g. VESTA:
[2]:
from ase.io import write
write("GaAs_prim.xsf", GaAs_prim)
write("GaAs_conv.xsf", GaAs_conv)
Now, to compare both structures (they should be identical), we import the FFingerPrint class and load the structures into the object.
[3]:
from aim2dat.strct import StructureCollection
strct_collection = StructureCollection()
strct_collection.append_from_ase_atoms("GaAs 216 prim", GaAs_prim)
strct_collection.append_from_ase_atoms("GaAs 216 conv", GaAs_conv)
Now we can calculate the f-fingerprint and compare the elemental contributions:
[4]:
from aim2dat.plots import PartialRDFPlot
plot = PartialRDFPlot()
plot.ratio = (10, 4)
plot.show_legend = True
plot.y_label = "F-Fingerprint"
element_fingerprints, atomic_fingerprints = strct_collection[
"GaAs 216 conv"
].calc_ffingerprint()
plot.import_ffingerprint("GaAs 216 conv", **element_fingerprints, x_unit="ang")
element_fingerprints, atomic_fingerprints = strct_collection[
"GaAs 216 prim"
].calc_ffingerprint()
plot.import_ffingerprint("GaAs 216 prim", **element_fingerprints, x_unit="ang")
plot.plot(["GaAs 216 conv", "GaAs 216 prim"])
[4]:
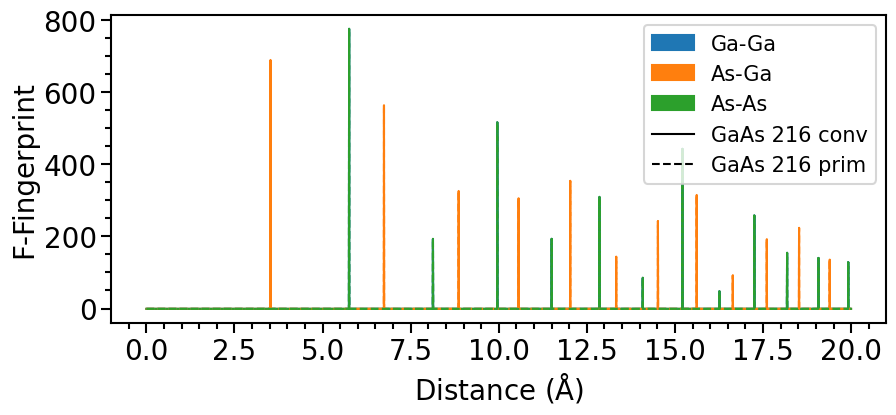
We can already see that both structures have the same fingerprints. Now we can also calculate the similarity of the two structures based on the cosine-distance:
[5]:
from aim2dat.strct import StructureOperations
strct_op = StructureOperations(structures=strct_collection)
strct_op.compare_structures_via_ffingerprint("GaAs 216 prim", "GaAs 216 conv", use_weights=True)
[5]:
1.1102230246251565e-16